The value of money is not constant. This is one of the principal facts on which the entire economic world is based. A rupee today will not be equal to a rupee tomorrow. Hence, a rupee borrowed today cannot be repaid by a rupee tomorrow. This is the basic need for the concept of interest. The rate of interest is used to determine the difference between what is borrowed and what is repaid.

Simple Intrest
Simple interest is calculated on the basis of a basic amount borrowed for the entire period at a particular rate of interest, the amount borrowed is the principal for the entire period of borrowing.

Compound interest

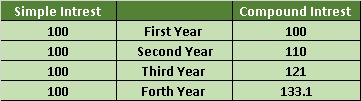
Compound interest The interest of the previous year/years is/are added to the principal for the calculation of the compound interest. The difference will be clear from the following illustration: A sum of rupees thousand at 10% per annum will have

TERMINOLOGIES PERTAINING TO INTEREST
-The man who lends money is the Creditor and the man who borrows money is the Debtor.
-The amount of money that is initially borrowed is called the Capital or Principal money.
-The period for which money is deposited or borrowed is called Time.
-The extra money, that will be paid or received for the use of the principal after a certain period is called the Total interest on the capital.
-The sum of the principal and the interest at the end of any time is called the Amount.

Amount = Principal + Total Interest.

The problems on Population change are similar to the problems on Compound Interest. The formulae applicable to the problems on compound interest also apply to those on population. The only difference is that in the application of formulae, the annual rate of change of population replaces the rate of compound interest. However, unlike in compound interest where the rate is always positive, the population can decrease. In such a case, we have to treat population change as we treated depreciation of value.

IMPORTANT FORMULAS
1) When the interest is compounded Annually:
Amount= P (1 + R/100) n

2)When the interest is compounded Half-yearly:
Amount = P (1 + (R/2)/100)2n

3)When the interest is compounded Quarterly:
Amount = P (1 + (R/4)/100)4n

4)When the rates are different for different years, say R1%, R2% and R3% for 1 year, 2 years and 3-year resp. Then,
Amount = P (1 + R1/100) (1 + R2/100) (1 + R3/100)

5)The present worth of ₹ x due n years hence is given by:
Present worth = x/ (1 + R/100)n

6)If a certain sum becomes “x” times in n years, then the rate of compound interest will be
R = 100(x1/n – 1)

7)If a sum of money P amounts to A1 after T years at CI and the same sum of money amounts to A2 after (T + 1) years at CI, then
R = (A2 – A1)/ A1 x 100

Compound Interest Installments
Let a person takes a loan from the bank at r% and agrees to pay the loan in equal installments for n years. Then, the value of each installment is given by
P = X/ (1 + r/100)n………X/ (1 + r/100)2 + X/ (1 + r/100)

For better understanding, let’s understand with the help of an example.

Question 1
One can purchase a flat from a house building society for ₹ 55000 or on the terms that he should pay ₹ 4275 as a cash down payment and the rest in three equal installments. The society charges interest at the rate of 16% p.a. compounded half-yearly. If the flat is purchased under an installment plan, find the value of each installment.

Solution
The cost of the flat is ₹ 55000. Now, if the person could either buy a flat by paying ₹55000 or
through an installment plan. Since the flat was purchased through an installment plan then the loan
amount = ₹55000 – 4275 (down payment) = ₹50725.
Here r = 16% compounded Half-yearly in 3 equal installments. Let x be the amount of
installment. Then,
₹50725 = x/ (1 + 16/200)3 + x/ (1 + 16/200)2 + x/ (1 + 16/200)
₹50725 = x (1/1.2591 + 1/1.1664 + 1/1.08)
₹50725 = x (0.79421 + 0.85722 + 0.9259)
₹50725 = x (2.577)
₹50725/2.5777 = x
x = ₹19683

Question 2
On a certain sum of money, compound interest earned at the end of three years = Rs. 1456. Compound interest at the end of two years is Rs. 880. Compute the principal invested.
Solution
(r2 + 3r + 3) x 440 = (r + 2) x 728
(r2 + 3r + 3) x 55 = (r + 2) x 91
55r2 + 165r + 165 = 91r + 182
55r2 + 74r -17 = 0
55r2 + 85r - 11r - 17 = 0
5r (11r + 17) -1 (11r + 17) = 0
r = 0.2 or a negative number. Or, r has to be 20%.
The question is " Compute the principal invested."
Rs. 2,000 is the principal amount.
Hence, the answer is Rs. 2000.

Question 3
Ram earns an interest of 600 over two years on a simple interest basis. On a compound interest basis, at the same interest rate, he would earn Rs. 630. What is the rate of interest?
Solution
Given, Interest on a simple interest basis is 600 for two years => Interest for one year is equal
to Rs 300.
If Ram invests the amount on a compound interest basis – then interest for the first year is
the same as investing in simple interest basis and that is equal to Rs 300.
Now, for CI we calculate interest on interest earned in previous time periods, whereas SI is
computed purely on the principal invested.
So, CI for second year is 630 – 300 = 330 and Rs30 is the interest earned on interest of 300
which amounts to 10%.
Therefore, rate of interest = 10%.
The question is "What is the rate of interest?"
10% is the rate of interest.
Hence, the answer is 10%

Question 4
What Principal amount will produce Rs. 500 as simple interest at an interest rate of 5% per annum in 6 years?
Solution
Total Interest Rate of Interest x Time
=6×5%
= 30%
Therefore, 30% = 500
Required principal Amount (100%) 500 / 30 x 100 = Rs. 1666.66