The CAT Trigonometry concepts with questions
CAT Trigonometry is one of the important topics for CAT preparation. It is part of geometry questions. Geometry questions contain 20% weightage in the CAT exam. However, no direct questions will be asked on trigonometry topic in CAT Question Paper but the basics will help you in solving geometry questions which have 20% weightage.
The basic concept of CAT Trigonometry
As you all know trigonometry involves formula-based problems to solve. Trigonometry is directly related to angles. For example 0°, 30°, 45°, 60°, and 90°.
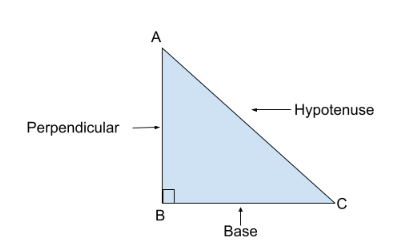
In above mention diagram AC represent hypotenuse. AB represent perpendicular. And BC represents the base of the triangle. Line AB has adjacent angle ∠A. And BC Side opposite angle ∠A. Hence on based on above mention information, we can say that.
- Sin A = sine of ∠A = (the side opposite to ∠A) / hypotenuse. This leads to (BC/AC)
- cos A = cosine of ∠A = (side adjacent to ∠A) / hypotenuse. This leads to (AB/AC)
- tan A = tangent of ∠A = (the side opposite to ∠A) / (side adjacent to ∠A). This leads to (BC/AB)
- cosec A = cosecant of ∠A. Hence formula is 1/ sin A
- sec A = secant of ∠A. Hence formula is 1/ cos A
- cot A = cotangent of ∠A. Hence formula is 1/ tan A
The CAT trigonometry table chart
Trigonometry is directly related to angles. For example 0°, 30°, 45°, 60°, and 90°. Learning the table will help you in solving problems. Let's have look at the table for more clarity.
| Ratio/ Angles | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| Sin θ | 0 | ½ | 1/√2 | √3/2 | 1 |
| Cos θ | 1 | √3/2 | 1/√2 | ½ | 0 |
| Tan θ | 0 | 1/√3 | 1 | √3 | ∞ or Undefined |
| Cosec θ | ∞ or Undefined | 2 | √2 | 2/√3 | 1 |
| Sec θ | 1 | 2/√3 | √2 | 2 | ∞ or Undefined |
| Cot θ | ∞ or Undefined | √3 | 1 | 1/√3 | 0 |
Trigonometry Fundamentals identities
Complementary Angle Theorem
If two acute angles add up. And there sum create 90°. Then you can say these types of angles are complementary. Co-functions of complementary angles are sine and cosine, tangent and cotangent, and secant and cosecant. The complementary angle theorem states that co-functions of complementary angles are considered to be equal. Let's have look at the table for more clarity.
- Sin (90 – A) = cos A
- Cos (90 – A) = sin A
- Tan (90 – A) = cot A
- Cot (90 – A) = tan A
- Sec (90 – A) = cosec A
- Cosec (90 – A) = sec A
For example cos 56° / sin 34°
Answer: The angles 56° and 34° are complementary. Use trigonometric ratios of complementary angles.
cos 56° / sin 34° = cos 56° / cos (90° - 34°)
cos 56° / sin 34° = cos 56° / cos 56°
Therefore cos 56° / sin 34° = 1
CAT trigonometry identities are
- sin2Ꝋ + cos2Ꝋ = 1
- tan2Ꝋ + 1 = sec2Ꝋ
- cot2Ꝋ + 1 = cosec2Ꝋ
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos²θ – sin²θ
- tan 2θ = 2 tan θ / (1 – tan²θ)
- cot 2θ = (cot²θ – 1) / 2 cot θ
Few more important formulas for CAT trigonometry
- sin(u + v) = sin(u)cos(v) + cos(u)sin(v)
- cos(u + v) = cos(u)cos(v) – sin(u)sin(v)
- sin(u – v) = sin(u)cos(v) – cos(u)sin(v)
- cos(u – v) = cos(u)cos(v) + sin(u)sin(v)
- tan(u+ v) = (tan(u) + tan(v))/ (1−tan(u) tan(v))
- tan(u- v) = (tan(u) − tan(v))/ (1+tan(u) tan(v))
CAT Trigonometry Problems sample
Ques. Anil looked up at the top of a lighthouse from his boat and found the angle of elevation to be 30 degrees. After sailing in a straight line 50 m towards the lighthouse, he found that the angle of elevation changed to 45 degrees. Find the height of the lighthouse.
a) 25
b) 25√3
c) 25(√3-1)
d) 25(√3+1)
Solution:

If we look at the above image, A is the previous position of the boat. The angle of elevation from this point to the top of the lighthouse is 30 degrees.
After sailing for 50 m, Anil reaches point D where the angle of elevation is 45 degrees. C is the top of the lighthouse.
Let BD = x
Now, we know tan 30 degrees = 1/ √3 = BC/AB
Tan 45 degrees = 1
=> BC = BD = x
Thus, 1/ √3 = BC/AB = BC / (AD+DB) = x / (50 + x)
Thus x (√3 -1) = 50 or x= 25(√3 +1) m.
Ques. If cos4θ - sin4θ = 3/4, then the value of 2cos2θ – 1 is:
Answer: 0.75
Explanation:
Given: cos4θ - sin4θ = ¾
We know that x2 − y2 = (x − y)(x + y)
So, (cos2θ − sin2θ)(cos2θ + sin2θ) = ¾
(cos2θ − sin2θ) = ¾
(cos2θ − 1 + cos2θ) = ¾
2cos2θ − 1 = 3/4
Ques. f sin(x + y) = cos(x – y), then the value of cos2x is:
Answer: ½
Explanation:
Given:
sin(x + y) = cos(x – y)
sin(x + y) = sin(90° – x + y)
x + y = 90° – x + y
2x = 90°
x = 45°
Therefore, cos2x = cos245° = = 1/2.
Also read: How to Prepare for CAT 2022
Few questions for practice.
Ques. Consider a regular hexagon TUVXYZ. There are towers placed at U and X. The angle of elevation from T to the tower at U is 30 degrees, and to the top of the tower at X is 45 degrees. What is the ratio of the heights of towers at U and X?
Options:
- 1:√3
- 1:2√3
- 1:2
- 3:4√3
Ques. Find the maximum and minimum value of 8 cos A + 15 sin A + 15
Options:
- 11√2+15
- 30; 8
- 32; -2
- 23; 8
Ques. If the sides 50 m and 130 m of the triangular field meet at an angle of 72°, then find the area in which wheat is cultivated. (sin 72° = 0.9510, cos 72° = 0.309)
Options:
- 100 pm
- 125 pm
- 160 pm
- None of these
Ques. If cos A + cos2 A = 1 and a sin12 A + b sin10 A + c sin8 A + d sin6 A - 1 = 0. Find the value of a+b/c+d
Options:
- 4
- 3
- 6
- 1
For CAT Quantitative section's full guidance visit this link- https://catking.in/best-guide-for-preparation-of-cat-quantitative-ability/
