CAT stands for common aptitude test. CAT Venn Diagram is important and useful in logical as well as quant section. This topic is an integral part of many competitive exams. An aspirants could except few questions from this topic. As Logical reasoning section contain a total of 20 questions and out of that few questions are from Venn Diagram . A Logical Reasoning & Data Interpretation contains 30% weightage in CAT exams.

Venn Diagram - Basic Concept

A rectangle representing the universal set starts with each Venn diagram. Then a circle represents each set of values in the problem. In the sections where the circles overlap, any values which belong to more than one set will be put. Venn diagram, also known as Euler-Venn diagram is a simple representation of sets by diagrams. The usual depiction makes use of a rectangle as the universal set and circles for the sets under consideration.

In CAT and other MBA entrance exams, questions asked from this topic involve 2 or 3 variable only. Therefore, in this article we are going to discuss problems related to 2 and 3 variables. Let's take a look at some basic formulas for Venn diagrams of two and three elements.

n ( A ∪ B) = n(A ) + n ( B ) - n ( A∩ B)
n (A ∪ B ∪ C) = n(A ) + n ( B ) + n (C) - n ( A ∩ B) - n ( B ∩ C) - n ( C ∩ A) + n (A ∩ B ∩ C )

And so on, where n( A) = number of elements in set A.
Once you understand the concept of Venn diagram with the help of diagrams, you don’t have to memorize these formulas.

Also read: CAT Preparation in 5 months : Toppers Strategy

Venn Diagram Symbols

The symbols used while representing the operations of sets are:

• Union of sets symbol: ∪
• Intersection of sets symbol: ∩
• Complement of set: A’ or A^c

Two Elements Venn Diagram.

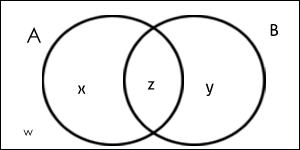
Where;
X = number of elements that belong to set A only
Y = number of elements that belong to set B only
Z = number of elements that belong to set A and B both (AB)
W = number of elements that belong to none of the sets A or B
From the above figure, it is clear that
n(A) = x + z ;
n (B) = y + z ;
n(A ∩ B) = z;
n ( A ∪ B) = x +y+ z.
Total number of elements = x + y + z + w

Three Element Venn Diagram.

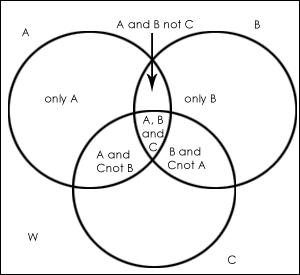
Where,
W = number of elements that belong to none of the sets A, B or C

Tip: Always start filling values in the Venn diagram from the innermost value.

The formula used to solve the problems on Venn diagrams with three sets is given below:

n(A ⋃ B ⋃ C) = n(A) + n(B) + n(C) – n(A ⋂ B) – n(B ⋂ C) – n(A ⋂ C) + n(A ⋂ B ⋂ C)

Venn Diagram of Set operations

In set theory, there are many operations performed on sets, such as:

• Union of Set
• Intersection of set
• Complement of set
• Difference of set

Properties of Set operations.

In set theory, there are many operations performed on sets, their properties are such as:

1. Properties of Complement of set:

• A ∪ A′ = U
• A ∩ A′ = φ
• (A ∪ B)′ = A′ ∩ B′
• (A ∩ B)′ = A′ ∪ B′
• U′ = φ
• φ′ = U

2. Properties of the intersection of sets operation:

• A ∩ B = B ∩ A
• (A ∩ B) ∩ C = A ∩ (B ∩ C)
• φ ∩ A = φ ; U ∩ A = A
• A ∩ A = A
• A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
• A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)

3. Some properties of Union operation:

• A ∪ B = B ∪ A
• (A ∪ B) ∪ C = A ∪ (B ∪ C)
• A ∪ φ = A
• A ∪ A = A
• U ∪ A = U

Video’s that could help aspirant.

Solved Examples

For Example 1: In a college, 200 students are randomly selected. 140 like tea, 120 like coffee and 80 like both tea and coffee.

• How many students like only tea?
• How many students like only coffee?
• How many students like neither tea nor coffee?
• How many students like only one of tea or coffee?
• How many students like at least one of the beverages?

Solution: The given information may be represented by the following Venn diagram, where T = tea and C = coffee.

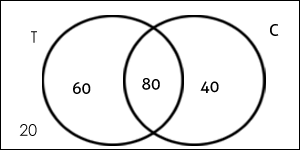
• Number of students who like only tea = 60
• Number of students who like only coffee = 40
• Number of students who like neither tea nor coffee = 20
• Number of students who like only one of tea or coffee = 60 + 40 = 100
• Number of students who like at least one of tea or coffee = n (only Tea) + n (only coffee) + n (both Tea & coffee) . So, 60 + 40 + 80 = 180

Few Past Years Questions

For Example 1.

Each of 74 students in a class studies at least one of the three subjects H, E and P. Ten students study all three subjects, while twenty study H and E, but not P. Every student who studies P also studies H or E or both. If the number of students studying H equals that studying E, then the number of students studying H is (CAT 2018)

Solution =

Let the number of students who studying only H be h, only E be e, only H and P but not E be x, only E and P but not H be y. Given only P = 0 All three = 10; Studying only H and E but not P = 20 Given number of students studying H = Number of students studying E

= h + x + 20 + 10

= e + y + 20 + 10

h + x = e + y total number of students = 74 Therefore, h + x + 20 + 10 + e + y = 74

h + x + e + y = 44 h + x + h + x = 44 h + x = 22

Therefore, the number of students studying H = h + x + 20 + 10 = 22 + 20 + 10 = 52.

For Example 2.

In a survey of 500 students of a college, it was found that 49% liked watching football, 53% liked watching hockey and 62% liked watching basketball. Also, 27% liked watching football and hockey both, 29% liked watching basketball and hockey both and 28% liked watching football and basketball both. 5% liked watching none of these games.

• How many students like watching all the three games?
• Find the ratio of the number of students who like watching only football to those who like watching only hockey.
• Find the number of students who like watching only one of the three given games.
• Find the number of students who like watching at least two of the given games.

Solution =

n(F) = percentage of students who like watching football = 49%

Then n(H) = percentage of students who like watching hockey = 53%

n(B)= percentage of students who like watching basketball = 62%

n ( F ∩ H) = 27% ; n (B ∩ H) = 29% ; n(F ∩ B) = 28%

Since 5% like watching none of the given games so, n (F ∪ H ∪ B) = 95%.

Now applying the basic formula,

95% = 49% + 53% + 62% -27% – 29% – 28% + n (F ∩ H ∩ B)

Solving, you get n (F ∩ H ∩ B) = 15%. Now, make the Venn diagram as per the information given.

Note: All values in the Venn diagram are in percentage.

The number of students who like watching all the three games = 15 % of 500 = 75. So The ratio of the number of students who like only football to those who like only hockey = (9% of 500)/(12% of 500) = 9/12 = 3:4.

The number of students who like watching only one of the three given games = (9% + 12% + 20%) of 500 = 205. The number of students who like watching at least two of the given games=(number of students who like watching only two of the games) +(number of students who like watching all the three games)= (12 + 13 + 14 + 15)% i.e. 54% of 500 = 270

Venn Diagram Questions

1. Out of 120 students in a school, 5% can play Cricket, Chess and Carroms. If so happens that the number of players who can play any and only two games are 30. The number of students who can play Cricket alone is 40. What is the total number of those who can play Chess alone or Carroms alone?
2. Draw the diagram that best represents the relationship among the given classes:
   Animal, Tiger, Vehicle, Car
3. At an overpriced department store, there are 112 customers. If 43 have purchased shirts, 57 have purchased pants, and 38 have purchased neither, how many purchased both shirts and pants?
4. In a group, 25 people like tea or coffee; of these, 15 like tea and 6 like coffee and tea. How many like coffee?

In sum for CAT Logical Reasoning & Data Interpretation section full guidance visit this link- https://catking.in/how-to-prepare-for-dilr-section-in-cat/

ENROL ON OUR COURSES NOW!

For CAT courses AND For Non-cat courses