Logarithm questions are generally direct, but the level of difficulty may be increased by adding the concept of the number of digits.
If x>0 and b is a constant (b≠1).In the equation y= log box, y is referred to as the logarithm, b is the base, and x is the argument.

When ax = N, then we say that x = logarithm of N to the base a and write it as x = logaN. In simple words, it represents the power to which a number must be raised. Let me expand on that by giving a simpler example.

If we are asked, what would be the result if ‘a’ is multiplied with itself ‘b’ times; then your answer would be x = a*a*a*…. b (times). This can also be written as a^b. This is also known as ‘a raised to the power of B
If we are asked, which number multiplied with itself ‘b’ times, will result in a; then you are asked for the value of x such that x*x*x*… b(times) = a

=> x^b = a
=> x = a^(1/b)
This is also known as ‘b th root of a’
If we are asked, how many times should you multiply ‘a with itself to get ‘b’, that is where the concept of logarithm comes into the picture. You are asked for the value of ‘x’ such that
a*a*a…. x (times) = b
=> x = Log a b
This is also known as ‘Log b to the base a’

An easy way to understand this is by:-
How many times should you multiply 2 with itself to get 8? Answer is Log 2 8 = 3
How many times should you multiple 5 with itself to get 625? Answer is Log 5 625 = 4
Another way to understand this would be:
If a x = N, then x = logaN
Where N is a POSITIVE number, “a” is a positive number OTHER THAN 1.

Since the log of a number is a value, it has 2 parts:
1. Integral part is known as the Characteristic
2. Decimal part is known as Mantissa

For example, Log 27 = 3 Log 3 = 3*0.4771 = 1.4313
In this case, the characteristic is 1 and the mantissa is 0.4313

There are 2 types of logarithms that are commonly used on the basis of bases:
1. Natural logarithm: base of the number is “e”.
2. Common logarithm: The base of the number is 10. When the base is not mentioned, it can be taken as 10.

The four properties of logarithms are given below:

1 )log_a (mn) = log_a m + log_a n
2 )log_a (m/n) = log_a m – log_a n
3 )log_a (m^n) = n log_a m
4 )log_b x = log_a x / log_ a b

Example:
3^4= 81 , log3 81 = 4.
log3 10 = ? ( given values of log3 2 and log3 5) log3 10 = log3 ( 2* 5) = log3 2 + log3 5.

SOME POINTS TO REMEMBER :

The Characteristic and Mantissa of a Logarithm The logarithm of a number consists of two parts: the integral part and the decimal part. The integral part is known as the characteristic and the decimal part is called the mantissa. For example, In log 3257 = 3.5128, the integral part is 3 and the decimal part is .5128; therefore, characteristic = 3 and mantissa = .5128. It should be remembered that the mantissa is always written as positive. Rule: To make the mantissa positive (in case the value of the logarithm of a number is negative), subtract 1 form an integral part and add 1 to the decimal part. Thus, –3.4328 = – (3 + .4328) = –3 – 0.4328 = (–3 –1) + (1 – 0.4328) = –4 + .5672. so the mantissa is = .5672

1. Characteristic of a number greater than unity for a common base is positive and is 1 less than the number of digits in an integral part.For example Characteristic of log 1000 = 3 which is 1 less than the number of digits in 1000.
2. For a number between 0 and 1, the characteristic is negative and its magnitude is 1 more than the number of zeros after the decimal point. For example : Characteristic of log 0.001 = -3.
3. log( x – y ) ≠ log x – logy
4. log( x + y ) ≠ log x + logy

The questions on logarithms are generally very direct but can be increased in difficulty level by introducing the concept of a number of digits. Firstly, have a look at the log values of some numbers ( base 10 ). The values are always mentioned in the question, but it is still advisable to memorize the values of numbers till 10

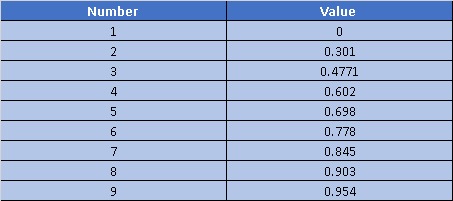
Let us find the number of digits in 3^ 100 .
x = 3 100
Log x = 100 Log^3
= 47.71
Number of digits here will be 47 + 1 = 48.
Logarithm Questions and Answers Based on Basic Concepts

Question(IIFT)
If an x = b y, then

a.) Log (a/b)= x/y
b.) Log(a) / log (b) = x/y
c.) Log(a) / log (b) = y/x
d.) None of these
Solution: option C is the correct answer
Take log on both sides to obtain the answer

Question( XAT 2014 )
The value of the expression ∑ 1 / log i 100! ( where i= 2 to 100 ) is

a.) 01
b.) 1
c.) 1
d.) 10
e.) 100
Solution: Option C is the correct answer.
The given expression is ∑ 1 / log I 100!
Expand the above expression.
= 1 / log1 100 ! + 1 / log2 100 ! + 1 / log3 100 ! + 1 / log4 100 ! + ……. + 1 / log100 100 !
Using logarithm property, the above expression becomes :
= log100! 2 + log100! 3 + …… + log100! 100
= log100! 2 * 3* 4 * …… 100
= log100! 100!
= 1

Question ( IIFT 2013 )
If log13log21 { √x+21 + √x } = 0, then the value of x is

a.) 21
b.) 13
c.) 81
d.) None of the above

Solution : log13log21 { √x+21 + √x } = 0
This implies, log21 { √x+21 + √x } = 130 = 1
√x+21 + √x = 21
By looking at the equation, we can see that x= 100.
Hence, option D is the correct answer.

Question
If 2 is the logarithm of a number to the base √3, then find out the logarithm of the same number for the base 3√3.

a.) 0
b.) ⅓
c.) ⅔
d.) 2
Solution: Option C is the correct answer.
Let the number be x.
log√3x = 2 3√3= (√3)3
log3√3x = ⅓ * 2 = ⅔

Question
log a (ab) = x , then log b(ab) is equal to :

a.) x/(x+1)
b.) 1/x
c.) x/(x-1)
d.) x/(1-x)
Solution: Option C is the correct answer.
Log (ab) / log a = x 1+ (log b / log a ) = x
Log b / log a = x – 1
Log a / log b = 1 / (x-1)
Add 1 to both sides and solve
Log (ab) / log b = x / (x-1)

Question
log9 (3log2 (1 + log3 (1 + 2log2x))) = 12. Find x.

a) 4
b) 12
c) 1
d) 2
Solution: Option D is the correct answer.
Log9 (3log2 (1 + log3 (1 + 2log2x)) = 12 3 log2(1 + log3(1 + 2log2x)) = 9 1/2
log2(1 + log3(1 + 2log2x) = 1 1 + log3(1 + 2log2x) = 2
log3(1 + 2log2x) = 1
log2x = 1
Hence,the value of x = 2 .

Question (XAT 2011)
The domain of the function f(x) = log7 { log3( log5(20x – x 2 – 91 ))} is
a.) (7,13)
b.) ( 8,12)
c.) (7,12)
d.) (12,13)
e.) None of these
Solution
f(x) = log7 { log3( log5(20x – x 2 – 91 ))}
For f(x) to be defined , log3( log5(20x – x 2 – 91 )) > 0
log5(20x – x 2 – 91 ) > 1
(20x – x 2 – 91 ) > 5
x 2 – 20x + 96 < 0
( x – 8 ) (x – 12) < 0
8 < x < 12
Hence, option B is the correct answer.

Question
If log { (x+y)/2 } = ½ (log x + log y), then which of the following is true ?

a.) x -y = 0
b.) x +y=0
c.) x +√y =0
d.) y +√x =0
Solution : log { (x+y)/2 } = ½ ( log XY)
log { (x+y)/2 } = log (x y)½
(x + y)/2 = √xy
Squaring both sides and simplifying,
(x-y)(x-y) = 0
Hence, a is the correct option.

Question
( log x )/ y-z = ( log y )/ z-x = ( log z )/ x-y , then x y z = ?

a.) 0
b.) 1
c.) 2 ( x- y- z)
d.) None of the above
Solution
Option b is the correct answer.
Let ( log x )/ y-z = k
Log x = k (y – z)
x= 10k(y-z)
Similarly , y = 10k(z-x) z= 10k(x-y)
Hence , x y z = 1.

Question
If l = 1+ log a b c, m = 1 + logb c a , n = 1 + logcab, then lmn = ?

a.) l2 + m2 + n2
b.) 1
c.) l + m+ n
d.) lm+ mn + nl
Solution: Option d is the correct answer.
l = 1+ log a b c can be written as l = logaabc
m = 1 + log b c a can be written as m = log b c a b
n = 1 + log c a b can be written as m = logcabc
1/ l = logabca , 1/ l = logabca , 1/ l = logabca
Add the above 3 expressions to get the correct answer.