“Probability is the logic of uncertainty and randomness. Uncertainty and randomness happen in just about every field of application and in daily life, so it is greatly useful and also fascinating to understand probability.” As a manager, it is an important topic that helps us learn the possibilities of success of a business decision for an organization. It helps us make better decisions by weighing the pros and cons of a judgment. It is always our goals with any decision, that the result of the decision we make today will be in our favor. The probability of an event is a number between 0 and 1. 0 means the event has absolutely no chance of occurring. While 1 means that the event is certain to happen. The higher the probability of an event, more is the likelihood of it occurring.

Event: Event refers to any outcome of an experiment that is independent of any other outcome and cannot occur simultaneously with another event.
Experiment: An action that can deliver some well-defined outcomes, is an experiment.
Random Experiment: “ If every trial of an experiment is carried out under identical conditions, and the outcome is not unique but maybe one of many possible outcomes then such experiment is known as a random experiment.”
Sample Space: The set of all probable outcomes in a Random Experiment is referred to as Sample space S, on the condition that no two of these outcomes can occur together and
precisely one of these results must happen whenever the experiment is carried out.
Certain and Impossible events: If S is a sample space, both S and the null set φ are events. S is termed as a certain event and φ is termed an impossible event.
Equally Likely Events: The given set of events is equally likely only when the occurrence of one event is not more probable than any other event.
Exhaustive events: In probability theory, a set of events is said to be exhaustive when at least one of the events in that set occurs every time the experiment is carried out. There is no other possible event outside the set of events. For example, flipping a coin has only two outcomes ie. head or tails. There is no other possibility.
Mutually Exclusive events: A set of events is said to be mutually exclusive when the occurrence of one event automatically means the impossibility of another event happening
on that experiment. Two events A and B are said to be mutually exclusive if AꓵB = φ.

Probability of an event: It essentially means during the execution of a random experiment the occurrence of any event is always random but a measure of its likely occurrence can be
calculated and that is known as the probability of the event.
The probability = 0; for a null event
The probability= 1 for a sure event
0 ≤ P(E)≤1 by definition

Question 1
If there are 10 boys and 5 girls in a class. Assuming a child does some mischief what is the probability
1.It has been done by a girl.
2. It has been done by a girl and a boy.
Solution
Probability = Favourable event / Total event
= 5 / 15
= 1 / 3
Answer 1/3
Probability = Favourable event / Total event
= 1/ 10 * 1/5
= 1/50
Answer 1/50

Probability while tossing a coin / Tossing n coins

Now if I ask you what is the probability of getting a Head when you toss a coin? Assuming the coin to be fair, you straight away answer 50% or ½. This is because you know that the outcome will either be head or tail, and both are equally likely. So we can conclude here:
Number of possible outcomes = 2
Number of outcomes to get head = 1
Probability of getting a head = ½
Probability of getting a tail = ½
If n coins are tossed whatever is the number of coins the denominator always becomes 2 n (Total Events)
If 2 coins are tossed it should be

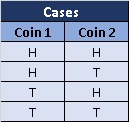
Question 2
What is the probability of atleast 1 head in toss of 2 coins
Solution
Probability = Favourable event / Total event
= 3/4
Answer 3/4

Question 3
What is the probability of atleast 2 head in toss of 3 coins.
Solution

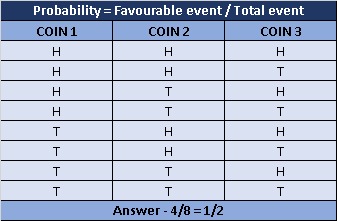
DICE

In probability, an event is a certain subset of the sample space. For example, when only one die is rolled, the sample space is equal to all of the values on the die, or the set (1, 2, 3, 4, 5, 6). Since the die is fair, each number in the set occurs only once. In other words, the frequency of each number is 1. To determine the probability of rolling any one of the numbers on the die, we divide the event frequency (1) by the size of the sample space (6), resulting in a probability of 1/6.Rolling two fair dice more than doubles the difficulty of calculating probabilities. This is because rolling one die is independent of rolling a second
one. One roll has no effect on the other. When dealing with independent events we use the multiplication rule. The use of a tree diagram demonstrates that there are 6 x 6 = 36 possible outcomes from rolling two dice.
If n dices are rolled
Whatever is the number of dices the denominator always becomes 6 n (Total Events)

Question 4
What is the probability of getting a prime number in throw of a dice.
Solution
Probability = Favourable event / Total event
Favourable event = { 2, 3 ,5}
Probability = 3/6 = 1/2
Answer 1/2

Question 5
What is the probability of getting sum less than 5 on throwing a pair of dice.
Solution
Probability = Favourable event / Total event
Sum <5 (Favourable event)
2 = { ( 1,1)}
3 = { (1,2) , (2,1)]
4 = { (2,2) , (3,1) , (1,3) }
Probability = 6 / 36
Answer = 1/6

Question 6
What is the probability of sum on two dices is an even number .
Solution
Probability = Favourable event / Total event
Sum even (Favourable event)
Total number of possible cases =36
Favourable cases of getting even number as the sum ={(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),(5,1),(5,3),(5,5),(6,2),(6,4),
(6,6)}
Total number of favourable cases =18
P(getting even number as the sum) = 18/36 = 1/2
Answer ½

Question 7
There are 7 boys and 8 girls in a class. A teacher has 3 items viz a pen, a pencil and an eraser, each 5 in number. He distributes the items, one to each student. What is the probability that
a boy selected at random has either a pencil or an eraser?
Solution
The probability of a boy being selected =7/15=7/15. Therefore, the probability of having either a pencil or an eraser with him =7/15 × 10/15=14 / 45

Question 8
A locker at the RBI building can be opened by dialling a fixed three digit code (between 000 and 999). Chhota Chetan, a terrorist, only knows that the number is a three digit number and has only one six. Using this information he tries to open the locker by dialling three digits at random. The probability that he succeeds in his endeavor is
Solution
Chhota Chetan knows that the code is a three digit number. Total number of numbers that can be formed = 3x(9x9x1) = 243. Of these only one number will open the locker.
The probability of his success = 1/243.