+91-8999-11-8999 (9 AM - 9 PM)
+91-7478-88-2888 (9 AM - 7 PM)
logo
Exams
More
arrow

Set theory & Function basic concepts for CAT

Set theory & Function basic concepts for CAT

Set theory & Function is an important topic for preparations. Set theory is most interesting concepts of mathematics. In fact , it will also helpful in data interpretation and logical reasoning section. An Aspirants should expect a few questions from Set theory. As quantitative section contain a total of 34 questions. Out of that few questions are from Set theory in CAT exams. A Set theory is contains graphs and properties.

Clearing your Set theory concepts will enhance your accuracy level in exams. Hence, Pay attention to concepts, graphs and properties. As you all know Set theory topics contain good weightage in the CAT exam. So That’s why this become an important topic for exams.

Formulas for Set Theory | PrepInsta

In this article, we learn about some of the important graphs and properties of CAT Set theory. All important aspects related to the topic will be covered. The aspirant would understand how to approach questions when his concepts become clear. In addition, one could easily ace Set theory just by properties, graphs and basic concepts clarity.

Also read: How to Prepare for CAT

Basic of Set Theory for CAT exam.

Set Theory is a branch of mathematical logic where we learn sets and their properties. A set is a collection of objects or groups of objects. These objects are often called elements or members of a set. For example, a group of players in a cricket team is a set.

Since the number of players in a cricket team could be only 11 at a time. Thus we can say, this set is a finite set. Another example of a finite set is a set of English vowels. But there are many sets that have infinite members. For instance set of natural numbers, a set of whole numbers, set of real numbers, set of imaginary numbers, etc.

Types of Sets

The sets are further categorised into different types, based on elements or types of elements. So Let’s have a look at the below mention different types of sets to understand with more clarity. These different types of sets in basic set theory are:

  1. Finite set: The number of elements is finite
  2. Infinite set: The number of elements are infinite
  3. Empty set: It has no elements
  4. Singleton set: It has one only element
  5. Equal set: Two sets are equal if they have same elements
  6. Equivalent set: Two sets are equivalent if they have same number of elements
  7. Power set: A set of every possible subset.
  8. Universal set: Any set that contains all the sets under consideration.
  9. Subset: When all the elements of set A belong to set B, then A is subset of B

Some Important laws of Set Theory for CAT exam.

So Let’s have a look at the below mention laws of set theory to understand with more clarity are:

  • COMMUTATIVE LAWS
  1. A B = B A
  2. A ∩ B = B ∩ A
  • ASSOCIATIVE LAWS
  1. (A B) C = A (B C)
  2. (A ∩ B) ∩ C = A ∩ (B ∩ C)
  • DISTRIBUTIVE LAWS
  1. A (B ∩ C) = (A B) ∩ (A C)
  2. A ∩ (B C) = (A ∩ B) (A ∩ C)
  • IDENTITY LAWS
  1. A = A
  2. A ∩ U = A
  • COMPLEMENT LAWS
  1. A Ac = U
  2. A ∩ Ac =
  • DE MORGAN’S LAW
  1. (A B)C = AC ∩ BC
  2. (A ∩ B)C = AC BC

Since we have now covered all the important formulas and concepts related to sets except one thing. For example Venn Diagrams, they are pictorial representation of sets and help in easily solving questions

VENN DIAGRAMS

A Venn diagram is a diagram that shows all possible logical relations between a finite collection of sets. They can be used to depict two sets, three sets, 4 sets or more. But for our purpose and level we only need their understanding up till four sets.

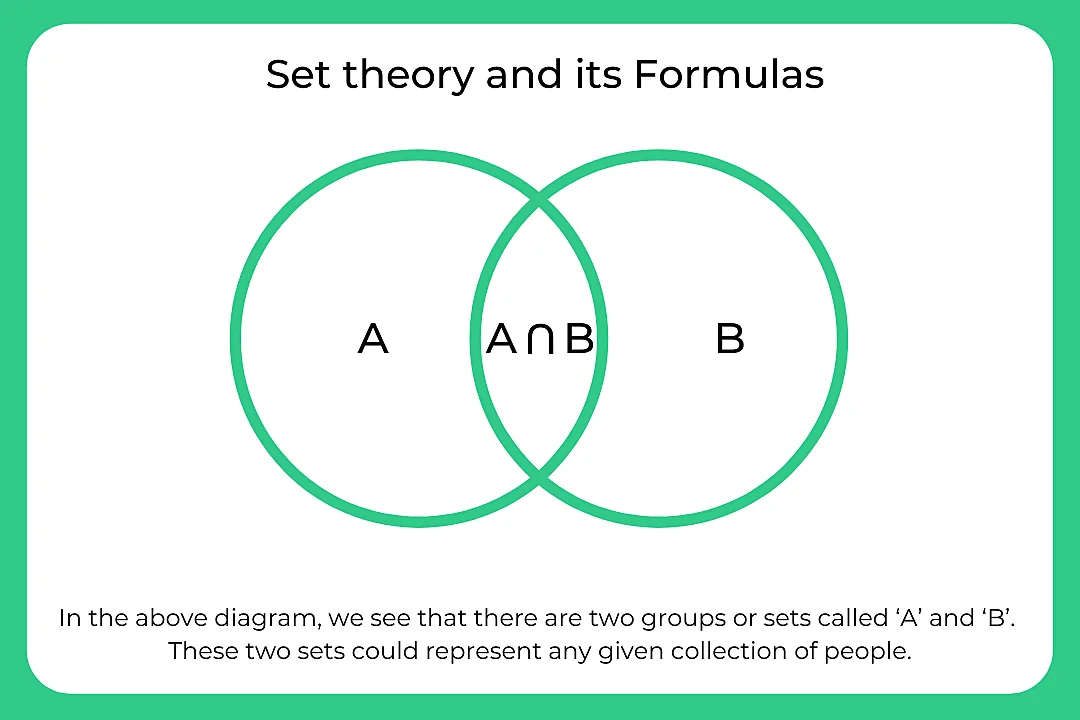
A two set Venn diagram is show as

set theory venn

The above diagram is called Venn Diagram where there are two sets A and B and U is the universal set.

VENN DIAGRAM FOR 3 SETS

A, B and C are three sets and U is the universal set. So Let’s have a look at the below mention venn diagram to understand with more clarity. So, the Venn diagram for 3 sets. Which is mention below

Set Operations for CAT exams.

The four important set operations that are widely shows. So Let’s have a look at the below mention as:

  • Union of sets
  • Intersection of sets
  • Complement of sets
  • Difference of sets

Fundamental Properties of Set operations:

So Like addition and multiplication operation in algebra, the operations such as union and intersection in set theory obeys the properties of associativity and commutativity. Also, the intersection of sets distributes over the union of sets.

Sets are used to describe one of the most important concepts in mathematics. For example functions. Everything that you observe around you, is achieved with mathematical models which are formulated, interpreted and solved by functions.

Set Theory Formulas for CAT exams.

So Let’s have a look at the below mention set theory formula's to understand with more clarity are:

  • n( A ∪ B ) = n(A) +n(B) – n (A ∩ B)
  • n(A∪B)=n(A)+n(B) {when A and B are disjoint sets}
  • n(U)=n(A)+n(B)–n(A∩B)+n((A∪B)c)
  • n(A∪B)=n(A−B)+n(B−A)+n(A∩B)
  • n(A−B)=n(A∩B)−n(B)
  • n(A−B)=n(A)−n(A∩B)
  • n(Ac)=n(U)−n(A)
  • n(PUQUR)=n(P)+n(Q)+n(R)–n(P⋂Q)–n(Q⋂R)–n(R⋂P)+n(P⋂Q⋂R)

Video’s that could help aspirant.

Solved example of Set Theory for CAT exam.

For example 1: If U = {a, b, c, d, e, f}, A = {a, b, c}, B = {c, d, e, f}, C = {c, d, e}, find (A ∩ B) ∪ (A ∩ C).

Solution: A ∩ B = {a, b, c} ∩ {c, d, e, f}

A ∩ B = { c }

=A ∩ C = { a, b, c } ∩ { c, d, e }

A ∩ C = { c }

Then (A ∩ B) ∪ (A ∩ C) = { c }

For example 2: Give examples of finite sets.

Solution: The examples of finite sets are: Set of months in a year

Set of days in a week

The Set of natural numbers less than 20

Hence, Set of integers greater than -2 and less than 3

For example 3: If U = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11}, A = {3, 5, 7, 9, 11} and B = {7, 8, 9, 10, 11}, Then find (A – B)′.

Solution: A – B is a set of member which belong to A but do not belong to B

∴ A – B = {3, 5, 7, 9, 11} – {7, 8, 9, 10, 11}

A – B = {3, 5}

According to formula, (A − B)′ = U – (A – B)

∴ (A − B)′ = {2, 3, 4, 5, 6, 7, 8, 9, 10, 11} – {3, 5}

So, (A − B)′ = {2, 4, 6, 7, 8, 9, 10, 11}.

Some question to practice Set Theory for CAT exam.

Question1: If ∪ = {1, 3, 5, 7, 9, 11, 13}, then which of the following are subsets of U.

Question2: Let A and B be two finite sets such that n(A) = 20, n(B) = 28 and n(A ∪ B) = 36, find n(A ∩ B).

Question3: In a group of 60 people, 27 like cold drinks and 42 like hot drinks and each person likes at least one of the two drinks. How many like both coffee and tea?

Question4: In a competition, a school awarded medals in different categories. 36 medals in dance, 12 medals in dramatics and 18 medals in music. So If these medals went to a total of 45 persons and only 4 persons got medals in all the three categories, how many received medals in exactly two of these categories?

For CAT Quantitative section’s full guidance visit this link- https://catking.in/best-guide-for-preparation-of-cat-quantitative-ability/

ENROL ON OUR COURSES NOW!

For CAT courses AND For Non-cat courses